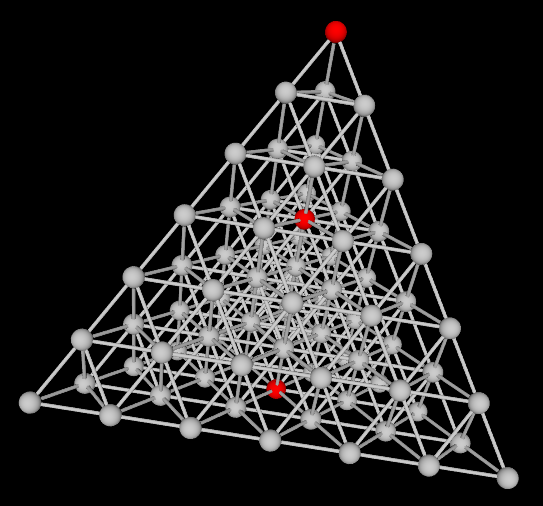
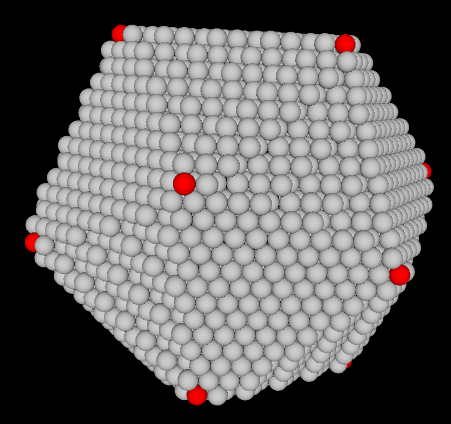
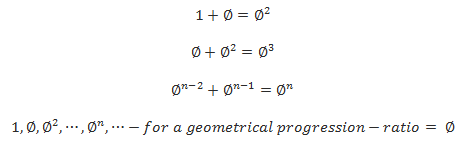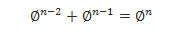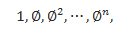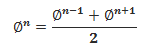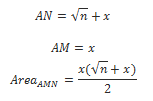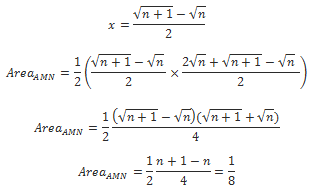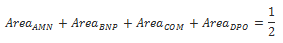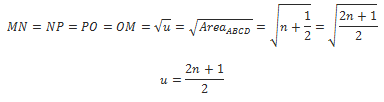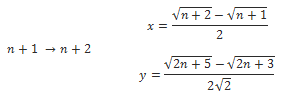CPS Geometry

Nick Trif

Version 1.0 - January 2017

  • 1. Assumptions

    Close Packed Singularity Geometry - or the CPS Geometry is the geometry built upon the following assumptions/axioms. The term axiom shall be understood in a slightly different way than in the classical Euclidian geometry. As we will see, this new geometry needs more than logic to derive its statements and facts.

  • 1.1 - Assumptions

    • A1: The point is the fundamental element. It shall be imagined as a perfect infinitesimal sphere.
    • A2: Once a point exist - it has the potential of generating a neighboring space around him. This neighboring space is composed of identical infinitesimal spheres.
    • A3: All the points/infinitesimal spheres from a neighboring space are obtained by translating the initial seed point. Rotation is not allowed.
    • A4: Multiple seed points can exist independently of each other, forming multiple neighboring spaces. The space is the combination of the neighboring spaces.

  • 1.2 - Notes

    • Close packing of spheres is the key to understanding and setting on a firm ground many shaky concepts and explanations from math, physics and science in general. I hope I’m able to start explaining what I mean in a way that makes sense to everyone.

    I will be very loose first – just to make the main idea easier to grasp:

    Let’s imagine that space is made-up from points. Science and math today consider points as being non-dimensional shapeless with no size and without any feature – no attributes – basically the points are nothing. In most people minds these points are something like very, very small dots on a sheet of paper. They are usually imagined as being circular – not that this will have any influence on the theory built on this nothingness.

    The points are sometimes defined as the end of line segments, or the intersection of two straight lines. With some logic one can infer that a line is made-up from an infinite number of points. If we imagine a mental experiment in which we have a line and intersect this line with any number of other lines, under any imaginable angles, the intersection is always a point; so the conclusion is that a line might be made up from points. But how these dimensionless points can form a line – which is called a "one dimension object"?

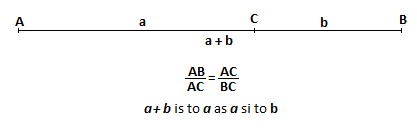
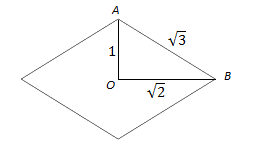
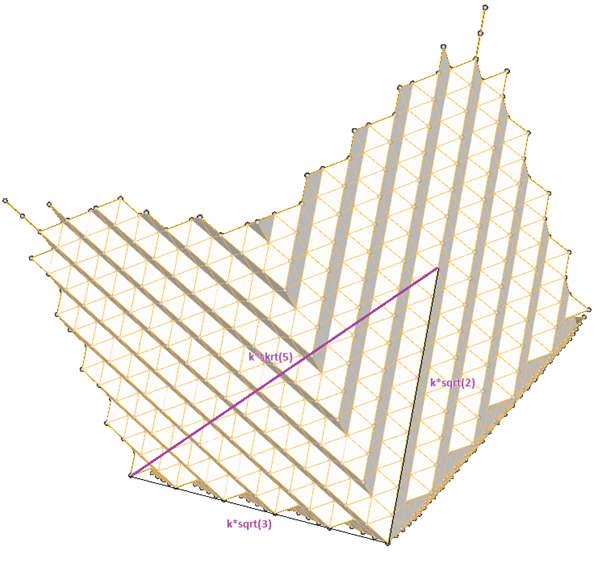
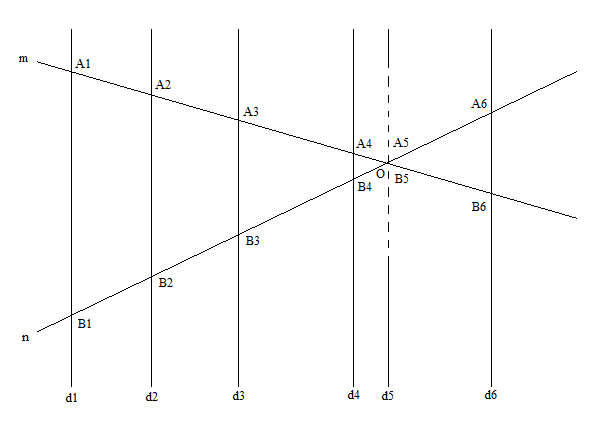
    What I propose is to think about points as spheres. We associate a shape to the points – even if we keep the size infinitely small. There is an argument in Leibnitz where he considers the ratios for a series of similar triangles – see Figure 1.1 below:

    Figure 1.1: Similar Triangles Argument
    Figure 1

    The argument goes like this:

    Let’s consider two lines (m) and (n) intersecting in point O. Let’s then consider another line (d) that translates – moves parallel relative to its initial position (d1) passing through all the points of (m) and (n). If A1, A2, … are the intersection of (d) and (m) and B1, B2, … are the intersection of (d) with (n), then all triangles OAB are similar:

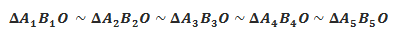
    Formula 001

    Leibnitz argues that the triangle formed when point A, B, and O overlap is similar with all the other ones – even if this is an infinitely small triangle. One can even write a relationship between the sizes of this infinitely small triangle:

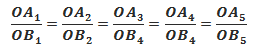
    Formula 002

    These days, using calculus (discovered by Leibnitz) we are used to the idea that zero divided by zero can be finite and a well-defined finite number.

    I propose a similar approach for the investigation of the features and structures of the physical space and matter in general. By extension this will also apply to the virtual spaces - used when analyzing and interpreting physical measurements or abstract quantities.

    The point I want to make by starting with the Leibnitz's example is that even if some quantities are zero (infinitesimally small) some ratios that involves these quantities have meaning and keep the values they have when the quantities are not zeros.

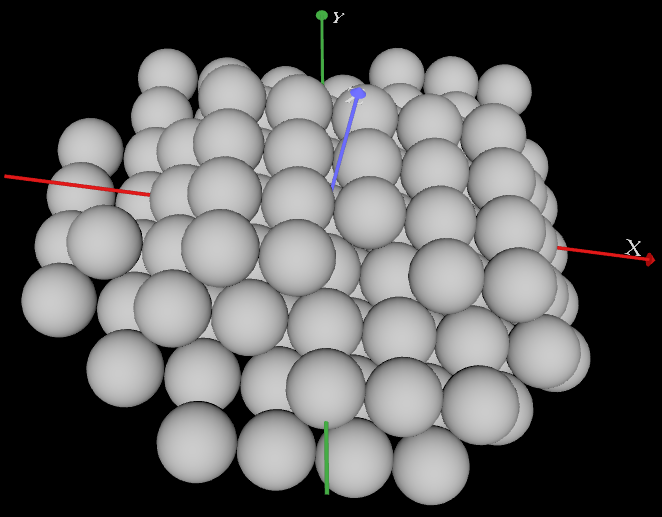
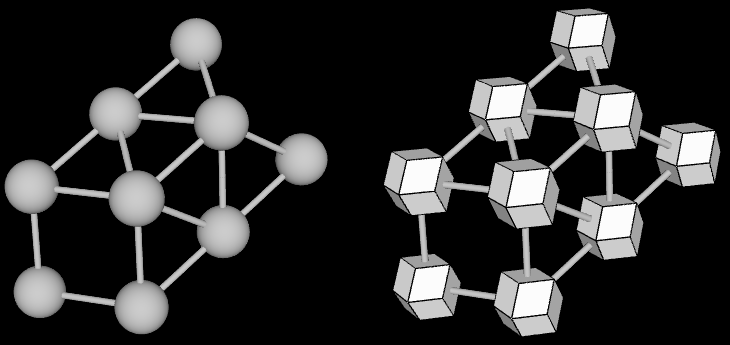
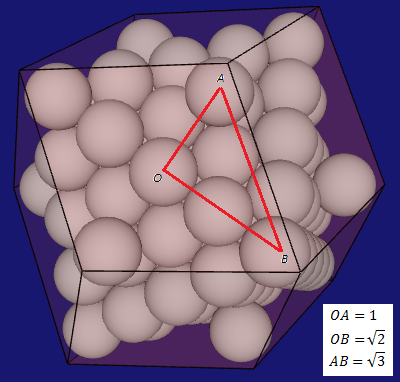
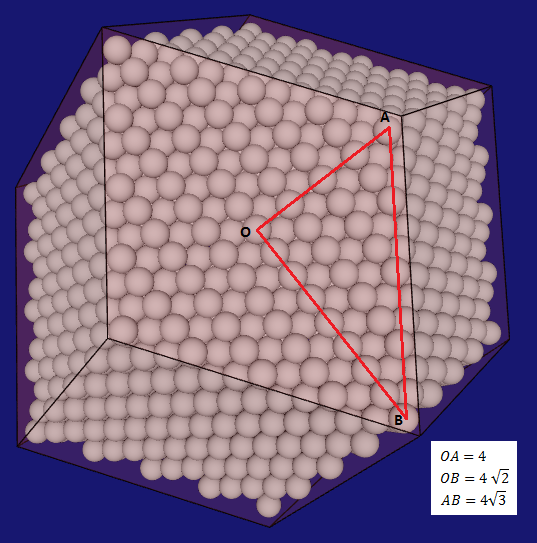
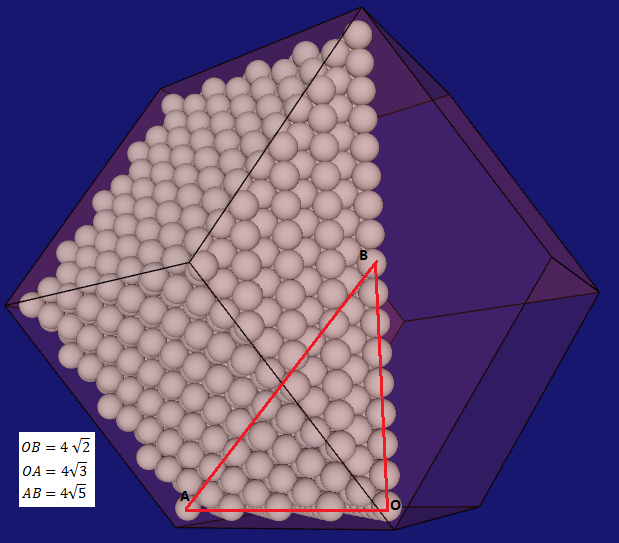
    Let’s imagine the points as being identical spheres – spheres with the same radius. The patterns, structures and properties discover in packing of spheres can be extended to the infinitely small domain – by the same argument described above.

    Extrapolating from here – the angle between two radiuses that joint the center of a sphere with the points of contacts on the sphere in the close-packing remain the same as when the spheres have some radius. The measurement of the angle is a ratio – so this makes totally sense and is consistent with the accepted results of the calculus.

    The measurement of an angle is always given by a ratio.

    The angles are equal in similar triangles – the sizes of triangles do not matter. The ratios are the way to express relationships between sizes.

    Why use spheres? A good way of responding to this question can be found in Amy C Edmondson book “A Fuller Explanation: The Synergetic Geometry of R. Buckminster Fuller”, 1987.

    On page 102 she writes:

    “The sphere's shape presents no corners, no angles - in short, no landmarks - by which to detect rotation or reflection. Its very shapelessness enables us to explore the shape of space. Furthermore, the total absence of angular form makes the precisely sculpted shapes generated by packing the identical "shapeless" units together all the more surprising. It is easy to see that individual spheres, as omni-symmetrical forms with neither surface angles nor specific facets to mold the form of clusters, cannot determine through their own shape the overall shape of packings. In conclusion, we are interested … in using spheres packing … as a medium through which spatial constraints can take visible shape.”

    It can be said that the sphere is the simplest object in the universe but it has an infinite potential of creating patterns.

    The sphere is the simplest mental object in terms of the way it is described. It is a featureless object. It has no lines, no corners, no faces, and no edges; it is just a close continuous surface with a constant curvature defined by its radius. It is in this context a one “dimension” object – defined by only one number – the radius.

    In the same time the sphere has the potential of creating all the possible geometrical patterns existing in the Universe – through the close packing. Isn’t this amazing?

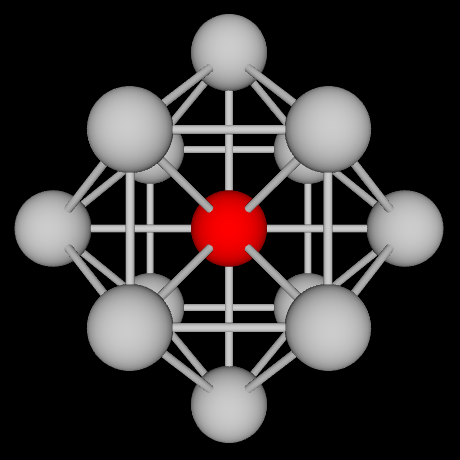
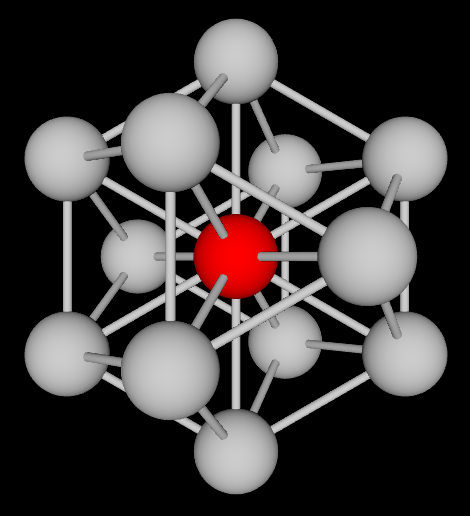
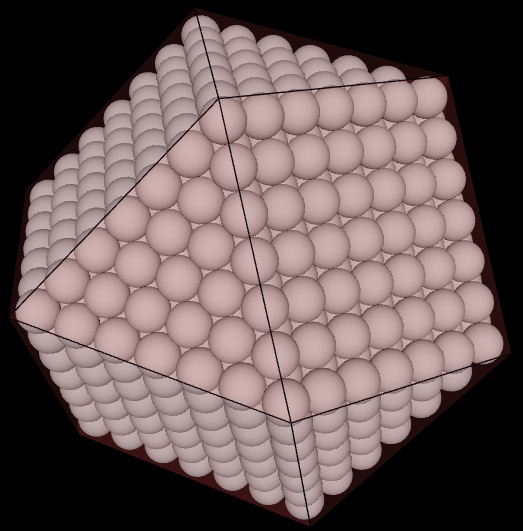
    Once a point comes into existence, it creates a potential neighboring space of empty spherical cells arranged according to the close-packing of sphere. Close packing of sphere is obtained by translating the initial sphere and filling-up the space - more on this on the next page. It has been shown that close-packing of spheres is the most efficient way of filling-up the space.

    Multiple independent points can generate their own potential neighboring spaces following the process described above. The relative position of two points from two sub-spaces is described by translation and rotation - a distance and an angle.

2. Introduction

Close Packing of Spheres (CPS)

Neils Bohr, a founding father of quantum theory, is reported to have said when presented with a pure mathematical argument: “No, no, you are not thinking, you are just being logical.”

In 1859 Riemann asked the question of how can we do math (and/or even science) – if we don’t use the method introduced by Euclid in geometry – start from a number of definitions and axioms – and using logical deduction “discover” all the propositions in the corresponding formal system. We have exhausted this method and it looks perfectly clear now that this approach has brought us to a dead end. Ask yourself what major discoveries happened in math and science in the last 100 years? And I mean real fundamental basic scientific discoveries.

The method that I propos next is probably best described as the mental-experimental method. We will imagine and do mental experiments (mental constructions and arrangements) to discover patterns and structures that can be generated by the close-packing of spheres. Following this method we will develop a new geometry.

These patterns or structures can always be assembled in the real world using just two types of elements - nodes and struts.

There are few ways of presenting and describing these mental-experimental patterns or structures.

The first method that comes to mind is to use words. Trying that, one can easily see that the number of words required for a complete description does not qualify this method as the best way to proceed. Some level of ambiguity will always be present when using such approach.

Next, one might want to consider images and/or diagrams. It has been said that an image is worth a thousand words. This is true, and this way of describing and presenting the patterns and structures generating by close packing of spheres proves to be a lot more efficient than using words. Having said that, the process of projecting more or less very complex 3-D structures on 2-D planes introduces a fundamental limitation – some information from the initial structure gets lost and is not available in the final image or diagram. There is still a level of ambiguity present in any figure or diagram that represents a close-packed structure or pattern.

These days we have at our disposal powerful tools to produce 3-D Visualizations and Animation of 3-D structures that theoretically are identical with the real objects. There is still some limitation with this - these 3-D models are virtual models. Very complex structures assembled from thousand of spheres, when seen on a 2-D screen, make it in some way cumbersome to manipulate and grasp the full information available. This is the preferred method used here to present the structures and patterns of the new geometry.

The best way to completely investigate structures and patterns that can be formed using close-packing of spheres (CPS) is to assemble and build real 3-D structures. Nothing compares with having a real structure in your hands. The best way to see complex structures with your mind is to play with the real structures using your hands. That's why we provide the components and instructions to help you to do this.

Virtual models of the close-packing structures are presenting and can be analyzed using combinations of the following type of tools:

1. Structures assembled from spherical nodes only - identified below as SS structures;

2. Structures assembled from rhombic dodecahedrons nodes only - identified below as RH structures;

3. Structures assembled from spherical nodes and struts and displayed as expanding structures - identified below as SS_ST structures;

4. Structures assembled from rhombic dodecahedron nodes and struts and displayed as expanding structures - identified below as RH_ST structures; and

5. Structures assembled from spherical nodes or rhombic dodecahedrons and struts and displayed with all the information required to support assembling them in real life. These structures are identified below as STR structures;

The use of the rhombic dodecahedron makes it easier to identify these structures as having patterns dictated by close-packing of sphere (CPS). The fact that each node of the structure is obtained by a translation from any other node can easily be seen with this approach."

Using struts allowed one to see inside these structures and reveal the interconnections that are hidden when using nodes only (spheres or rhombic dodecahedrons).

Let's proceed.

  • 2.1 Square Lattice

    Identical spheres can be arranged in a square pattern on a plane surface. In such arrangement each sphere has exactly four neighbors in a plane. By connecting, with imaginary lines, the contact points between any two spheres one can easily see a square pattern being formed. Due to the fact that in such an arrangement each sphere could have up to four neighbors - we will refer to this arrangement as the square lattice pattern - see Figure 2.1 below:

    Figure 2.1: Square Lattice
    Figure 2.1

    Explore the links below for a better understanding of these facts:

  • 2.2 Hexagonal Lattice

    Identical spheres can also be arranged in a hexagonal pattern on a plane surface. In such arrangement each sphere has exactly six neighbors in a plane. By connecting, with imaginary lines, the contact points between any two spheres one can easily see a hexagonal/triangular pattern being formed. Due to the fact that in such an arrangement each sphere could have up to six neighbors - we will refer to this arrangement as the hexagonal lattice pattern – see Figure 2.2 below:

    Figure 2.2: Hexagonal Lattice
    Figure 2.2

    Explore the links below for a better understanding of these facts:

  • 2.3 Close-Packing of Spheres (CPS) - Square Lattice Case

    Starting from a plane with a square lattice pattern one can stack a second plane with a square lattice pattern on top of the first plane. To obtain the best arrangement possible one has to translate the second plane along a direction that forms a 45 degrees angle with the directions of the square pattern of the first plane until the two planes are as close as possible (until the distance between the two planes is as small as possible). When this is done each sphere of the second plane is in contact with exactly four spheres from the first plane.

    One can continue this process and stack a third plane with a square lattice pattern on top of the second one following exactly the approach described above. By doing this, one can see again that any sphere of the third plane touches exactly four spheres from the second plane.

    Any sphere from this arrangement is in direct contact with:

    - four spheres from the plane below the plane containing the sphere being considered;

    - four sphere from the same plane containing the sphere being considered; and

    - four spheres from the plane above the plane containing the sphere being considered.

    The patterns of the top plane and the bottom plane are exactly above each other - there is no translation between these two planes.

    Following the process described above one ends up with an arrangement known as the close-packing of spheres (CPS). In this arrangement all spheres have exactly twelve neighbors – see Figure 2.3 below:

    Figure 2.3: Close Packing of Spheres - Case 1
    Figure 2.3

    Explore the links below for a better understanding of these facts:

  • 2.4 Close-Packing of Spheres (CPS) - Hexagonal Lattice Case

    On the necessity of choosing the best, Leibnitz writes the following:

    “Let us assume three points are given, so that from those a triangle may be formed: I say that a wise man will form from those an equilateral triangle (if there is no special reason for acting otherwise), for thus all points are treated in the same way. And the species of equilateral triangle is lowest i.e. all equilateral triangles are similar to each other. If the necessity to choose the best, which is in the wise man, would destroy freedom, it would follow that neither does God act freely, since for many things he chooses the best. The essences of things are like numbers. Just as two numbers are not equal to each other, so no two essences are equally perfect.”

    Starting from a plane with a hexagonal lattice pattern, one can stack a second plane with a hexagonal lattice pattern on top of the first plane. To obtain the best arrangement possible one has to translate the second plane along a direction that form a 60 degrees clockwise angle with the directions of the hexagonal pattern of the first plane until the two planes are as close as possible (until the distance between the two planes is as small as possible). When this is done each sphere of the second plane is in contact with exactly three spheres from the first plane.

    One can continue this process and stack a third plane with a hexagonal lattice pattern on top of the second one following exactly the approach described above, but with a small change. The translation is done this time along a direction that forms a 60 degrees counterclockwise angle with the directions of the hexagonal pattern of the first plane. By doing this, one can see again that any sphere of the third plane touches exactly three spheres from the second plane.

    Any sphere from this arrangement is in direct contact with:

    - three spheres from the plane below the plane containing the sphere being considered;

    - six sphere from the same plane containing the sphere being considered; and

    - three spheres from the plane above the plane containing the sphere being considered.

    The patterns of the top plane and the bottom plane are not identical anymore - more about this in the next sections.

    Following the process described above one ends up with the same close-packing of spheres arrangement encounter in the previous section – see Figure 2.4 below:

    Figure 2.4: Close Packing of Spheres - Case 2
    Figure 2.4

    Explore the links below for a better understanding of these facts:

  • 2.5 Twelve Neighbors - Square Lattice

    The best way to start understanding the structure of these close packing arrangements is o look at a sphere from the pattern and its twelve neighbors – see Figure 2.5 below:

    For the square lattice case of generating the close packing pattern it can be seen that there is a periodicity modulo 2 for the patterns of the planes:

    - planes 0, 2, 4, ... are identical when place on top of each other;

    - planes 1, 3, 5, ... are also identical when place on top of each other; and

    - a translation of 45 degrees separates the two types of planes.

    Figure 2.5: My Twelve Neighbours - Square Lattice
    Figure 2.5

    Explore the links below for a better understanding of these facts:

  • 2.6 Twelve Neighbors - Hexagonal Lattice

    For the hexagonal lattice case of generating the close packing pattern it can be seen that there is a periodicity modulo 3 for the patterns of the planes:

    - planes 0, 3, 6, ... are identical when place on top of each other;

    - planes 1, 4, 7, ... are also identical when place on top of each other;

    - planes 2, 5, 8, ... are also identical when place on top of each other; and

    - a translation of 60 degrees clockwise or counter-clock wise separates the three types of planes.

    It should be mentioned again that these two patterns are in fact the same one - they are just seen from different angles.

    There is only one close-packing of sphere arrangement/structure. Square lattice patterns and hexagonal lattice patterns are both seen in this arrangement. As we will see later, these are the simpler and the most obvious patterns one can discover in this arrangement – see Figure 2.6 below:

    Figure 2.6: My Twelve Neighbors - Hexagonal Lattice
    Figure 2.6

    Explore the links below for a better understanding of these facts:

    Another way of looking to this periodicity is to observe to the planes of a tetrahedron assembled from spheres. The planes having a central sphere obey the following pattern: Yes-No-No-Yes-No-No-Yes - see Figure 2.6-1 and the links below:

    Figure 2.6-1: Central Sphere Pattern
    Figure 2.6-1

  • 2.7 Square Lattice Planes

    As seen above, one way of generating the close-packing of spheres arrangement is to stack parallel square lattice planes (with the required translation between planes).

    A relatively short investigation reveals that there are two more directions in the close-packing that holds stacks of parallel planes with the same underlining square lattices. These three directions are mutually perpendicular forming the well-known planes of the 3-D Cartesian coordinate system. These set of planes are parallel with the three distinct planes that form a cube.

    The dedicated term used to express the relationships among the directions of these three planes is orthogonal. These three planes are orthogonal.

    Explore the following links to see how these three orthogonal planes appear in the CPS.

  • 2.8 Hexagonal Lattice Planes

    A similar investigation of the CPS arrangement, as the one presented in the previous section, reveals that there are four directions in the close-packing that hold stacks of parallel planes with an underlining hexagonal pattern of spheres.

    For consistency with the orthogonal planes defined above we will introduce a new term yo express the relationships among the directions of these four sets of planes. We will say that these four planes are tetrahegonal to each other. Of course, these four set of planes are parallel with the planes of a tetrahedron.

    Explore the following links to see how these four tetrahegonal planes appear in the close packing of sphere.

  • 2.9 Axis

    The process of defining a coordinate system corresponding to the 3-D Cartesian system can be further developed with the introduction of three orthogonal axes as presented in the links below.

    It is time to start hinking outside the proverbial box, or better said - outside the Cartesian box. Observe that these three axes are lines - but they are formed by a more complex pattern - but still a line pattern – see Figure 2.9 below:

    Figure 2.9: Orthogonal Axes System
    Figure 2.9

    Explore the links below to get a visual representation of these three orthogonal axes.

    A similar set of coordinate system can also be developed for the set of planes based on a hexagonal lattice pattern. Corresponding to these four planes there are four tetrahegonal axes.

    Again, these axes are lines, but they are formed by a different pattern than the pattern encountered in the orthogonal case described above – see Figure 2.9-1 below:

    Figure 2.9-1: Tetrahegonal Axes System
    Figure 2.9-1

    Explore the links below to get a visual representation of these four tetrahegonal axes.

    A more complete coordinate system can be imagined. In this case there are seven different planes - three having an underlining square lattice patterns and four a hexagonal lattice patterns.

    There are also seven axes - the first three mutually orthogonal on each other and remaining four mutually tetrahegonal on each other – see Figure 2.9-2 below:

    Figure 2.9-2: Seven Axes System
    Figure 2.9-2

    As said above, there are two types of planes patterns and two types of lines patterns (corresponding to the square lattice pattern and hexagonal lattice pattern).

    Explore the following links to get a better understanding of this combined coordinate system.

  • 2.10 What's Next?

    What was presented in this introduction is just the tip of the iceberg of the patterns and facts hidden in the CPS arrangement.

    For us, to be fully comfortable and convinced with the idea that we should replace the Cartesian plane and Cartesian space with a geometry resulting from CPS, namely with a space that has au underlining CPS spatial lattice, we need, at a minimum to show/demonstrate the following:

    • 1. All the five platonic perfect bodies (including the icosahedrons and dodecahedron) have a "natural" existence in this space. Theirs patterns can be found in the close packing of spheres. - Section 3: Platonic Solids ;


    • 2. The minimum surfaces (discovered as patterns in close-packing) – are the domain of complex plane. Patterns can be found that prove and extend the laws determined experimentally by Joseph Plateau regarding the manifestations of minimum surfaces - Section 4: Minimum Surfaces;


    • 3. The Archimedean solids and any polyhedron also have a "natural" existence in this space. - Section 5: Archimedean Solids;


    • 4. There is a connection between the Golden section and Fibonacci sequence - Section 6: Fibonacci Sequence; and


    • 5. There are facts in the CPS that provide another kind of explanation of the validity of the Pythagorean Theorem - Section 7. Pythagorean Theorem.


    Coming from the other side, the philosophical and dialectical approach to science, shall also work. Three principles guided me during the investigation and development of these ideas:

    • 1. The principle of minimum action – or the best solution argument – everything is done and exists in the best way possible – see Leibnitz and Plato for more about this and about the “final cause” in nature;


    • 2. Plato's theory of ideas – best described by the following statement: “Beauty makes beautiful things beautiful.” In my mind this has a direct connection with prime numbers, multiplication and power; and


    • 3. The process of dialectics as described also by Plato. This justifies the process of going from spheres to close-packing to simple patterns in CPS and finally to patterns of patterns (meta-patterns) – as the higher place of understanding.


3. Platonic Solids

Tetrahedron, Octahedron, Cube, Icosahedron and Dodecahedron

I would like to start with an argument from The Republic - by Plato (Translated by Benjamin Jowett) - about the need of a Space Geometry, or a Solid Geometry - as Socrates refers to it. It goes like this:


"After plane geometry, I said, we proceeded at once to solids in revolution, instead of taking solids in themselves; whereas after the second dimension the third, which is concerned with cubes and dimensions of depth, ought to have followed.

That is true, Socrates; but so little seems to be known as yet about these subjects.

Why, yes, I said, and for two reasons:—in the first place, no government patronises them; this leads to a want of energy in the pursuit of them, and they are difficult; in the second place, students cannot learn them unless they have a director. But then a director can hardly be found, and even if he could, as matters now stand, the students, who are very conceited, would not attend to him. That, however, would be otherwise if the whole State became the director of these studies and gave honour to them; then disciples would want to come, and there would be continuous and earnest search, and discoveries would be made; since even now, disregarded as they are by the world, and maimed of their fair proportions, and although none of their votaries can tell the use of them, still these studies force their way by their natural charm, and very likely, if they had the help of the State, they would someday emerge into light.

Yes, he said, there is a remarkable charm in them. But I do not clearly understand the change in the order. First you began with a geometry of plane surfaces?

Yes, I said.

And you placed astronomy next, and then you made a step backward?

Yes, and I have delayed you by my hurry; the ludicrous state of solid geometry, which, in natural order, should have followed, made me pass over this branch and go on to astronomy, or motion of solids.

True, he said.”


There is a belief in the minds of many that must be something mystical about platonic solids and all the other semi-regular solids. In the minds of some others, which are more sophisticated and mathematical inclined, there are a lot of irrational numbers that somehow they can use to make some sense of the existence of these polyhedrons. It looks a bit magical for them – but they are relatively happy with their understanding of the platonic solids and all the other semi-regular solids and the conclusions derived from them. I was a proud member of the second group – for a very long time.

What I’m going to show next, using the close-packing of spheres, is that all the complexity and magic, all the irrational numbers of lengths and angles of these polyhedrons have one underling principle – they all can be assembled (constructed) and described by the right arrangement and with the right number of identical spheres – or rhombic dodecahedron for that matter. I prefer in a way the rhombic dodecahedron due to the fact that the angles are clearly seen and the fact that no rotations of the nodes are needed appears clearer.

British Dictionary gives the following definition for "proof:"

" any evidence that establishes or helps to establish the truth, validity, quality, etc, of something"

Euclidian geometry is based on demonstrations as the method of establishing the truth of its propositions.

One doesn’t need any proof to show that something exists if one is holding it in his hands and see it with his eyes. The 3-D models of the platonic solids presented below and their corresponding real 3-D structures one can assemble, are the only proof one need for their existence. The proof is in the pudding.

The patterns for the first three platonic structures, namely tetrahedron, octahedron and cube can be discovered relatively easily in the CPS. The next three subsections present few variants of these structures.

The Eureka Moment that gave birth to this geometry happened when I was able to see the icosahedron pattern well-hidden inside the CPS. Subsection 4 covers some structures based on icosahedron in relatively great details.

Knowing that the dodecahedron is the dual of the icosahedron provides the path to the dodecahedron structure. This pattern is presented in subsection 5.


4. Minimum Surfaces

Rhombic Dodecahedron

CPS needs only one type of element to exist - the sphere. When large numbers of spheres are packed together in a CPS arrangement - patterns or structures start appearing. These patterns manifest in real life as solids - or as 3-D objects. As we have shown in the previous section, all five platonic solids have a well-defined existence in the CPS and consequentially in the real life.

It is now the time to expand this geometry with the introduction of the concept of the surface.

Let's do that by going back to Plato and read the following exchange between Socrates and Meno in "Meno" – by Plato (Translated by Benjamin Jowett:)

“SOCRATES: Well, I will try and explain to you what figure is. What do you say to this answer?—Figure is the only thing which always follows colour. Will you be satisfied with it, as I am sure that I should be, if you would let me have a similar definition of virtue?

MENO: But, Socrates, it is such a simple answer.

SOCRATES: Why simple?

MENO: Because, according to you, figure is that which always follows colour.

(SOCRATES: Granted. )

MENO: But if a person were to say that he does not know what colour is, any more than what figure is—what sort of answer would you have given him?

SOCRATES: I should have told him the truth. And if he were a philosopher of the eristic and antagonistic sort, I should say to him: You have my answer, and if I am wrong, your business is to take up the argument and refute me. But if we were friends, and were talking as you and I are now, I should reply in a milder strain and more in the dialectician's vein; that is to say, I should not only speak the truth, but I should make use of premises which the person interrogated would be willing to admit. And this is the way in which I shall endeavour to approach you. You will acknowledge, will you not, that there is such a thing as an end, or termination, or extremity? —all which words I use in the same sense, although I am aware that Prodicus might draw distinctions about them: but still you, I am sure, would speak of a thing as ended or terminated—that is all which I am saying—not anything very difficult.

MENO: Yes, I should; and I believe that I understand your meaning.

SOCRATES: And you would speak of a surface and also of a solid, as for example in geometry.

MENO: Yes.

SOCRATES: Well then, you are now in a condition to understand my definition of figure. I define figure to be that in which the solid ends; or, more concisely, the limit of solid. ”

Let's review the type of faces encountered so far when we discovered and studied the platonic solids. Considering that the underlining lattice determines the nature of a surface, these surfaces are:

1. Surfaces with an underlining hexagonal lattice - see faces of tetrahedron, octahedron and the eight faces of the icosahedron as illustrated in Figure 4.0 below:

Figure 4.0: Hexagonal Lattice Based Surface
Figure 4.0-0

2. Surfaces with an underlining square lattice - see faces of cube as illustrated in Figure 4.0-1 below:

Figure 4.0-1: Square Lattice Based Surface
Figure 4.0-1

3. Surfaces with an underlining pentagonal lattice. These faces have been encountered when studying the pentagonal faces of the dodecahedron - see it again in Figure 4.0-2:

Figure 4.0-2: Pentagonal Lattice - CPS Pattern
Figure 4.0-2

4. Surfaces with an underlining icosahedron type 2 lattice. These faces have been encountered when studying the faces of the icosahedron that do not have a hexagonal underlining lattice - see Figure 4.0-3 below:

Figure 4.0-3: Icosahedron Type 2 Lattice - CPS Pattern
Figure 4.0-3

In this section a new type of lattice will be uncovered and facts are provided that link the surfaces with this underling lattice to the minimum surfaces observed in real life when playing with soap films.

5. Archimedean Solids

Miscellaneous CPS Structures

In addition to the five platonic solids, there are other 13 solids known as Archimedean solids that are well-known in geometry.

The initial purpose of this section was to provide the CPS patterns for each of these solids. Currently only the patterns of few of these solids are available for publishing on this site. Future releases of this document will include more of these semi-regular solids.

All these patterns are possible and exist in the CPS. Most of these Archimedean solids can be obtained by some simple cuts of the platonic solids or other archimedean solids. These cuts can be done through the middle of the sides, or at some distance from the vertexes.

This section also contains some other CPS structures that add points to the argument of an underlying CPS lattice to the 3-D physical space.

6. Fibonacci Sequences

The Golden Section in CPS

"Geometry has two great treasures; one is the Theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold; the second we may name a precious jewel." Johannes Kepler

  • 6.1 The Golden Ratio

    A lot has been written over the years about the golden ratio, the golden section, or the golden number. I will just mention here few facts about the golden ratio to help with the understanding of the connection between this ratio and the CPS.

    There are at least three ways the golden ratio is defined in Euclidian geometry:

    1. The division of a line segment into the extreme and mean ratio – so that the whole segment is to the greater segment as the greater segment is to the smaller segment - see Figure 6.1 below:

    Figure 6.1: Golden Ratio - Definition 1
    Figure 6.1

    2. The ratio between the length of diagonal and the side of a regular pentagon - see Figure 6.1-1 below:

    Figure 6.1-1: Golden Ratio - Definition 2
    Figure 6.1-1

    3. As a method of constructing an icosahedron by connecting the vertices of three othogonal golden rectangles - see Figure 6.1-2 below:

    Figure 6.1-2: Golden Ratio - Definition 3
    Figure 6.1-2

    A better way to express this is by saying: "A father is to his son as his son is to his grandson, and as his father was to him."

    Of course this is 100% true – but some people will say “it is fuzzy” . This is in fact the main characteristic of the mind – the power to find those un-grasped qualities that make similar things – similar, similar situations – similar, similar relationships – similar.

  • 6.2 The Golden Number And The Arithmetic Geometric Mean (AGM)

    The Arithmetic Geometric Mean (AGM) was heavily used by Gauss for computing the elliptical integrals and has since been employed in developing many numerical algorithms, including the ones used for the calculation of PI.

    Let's mention some a remarkable fact about the golden number - the sum of two consecutive terms determine the next term

    Formula 003

    From here we see that the terms of the power of golden number sequence have double properties:

    1. An additive relationship that can be seen as a modified arithmetic progression:

    Formula 004

    2. A multiplicative relationship – defined by the fact that the terms form a geometrical progression.


    Every member of the sequence:

    Formula 005

    1) is the arithmetic mean of the previous and next terms:

    Formula 006

    See demonstration below:

    Formula 007

    2. But also every term in the sequence is the geometric mean of the previous and next term:

    Formula 008

    So every member of the sequence is the Arithmetic Geometric Mean (AGM) of the previous term and next term.


  • 6.3 Fibonacci Sequences

    Another way of defining the golden number is using the Fibonacci sequence defined as:

    Formula 009

    The limit of the ratio of two consecutive terms in the Fibonacci sequence defines the golden number:

    Formula 010

    The Fibonacci sequence can be started using any two numbers. The limit of the ratio of consecutive terms is always the golden number.


  • 6.4 The Golden Number CPS Equivalent - Icosahedrons Patterns in CPS

    The existence of the icosahedron patterns in the CPS provides a way of defining ratios of natural numbers that have a similar geometrical interpretation to the golden number defined in the Euclidian plane. Following this approach, the golden number is the limit of these ratios defined in CPS.

    The third definition of the golden section given in section 6.1 above (as a method of defining the icosahedron by the vertices of three golden rectangles) can easily be applied to the icosahedron pattern in CPS.

    The icosahedron pattern in the CPS can be imagined as being formed by three mutually orthogonal CPS golden rectangles. Figure 6.4 shows the icosahedron pattern and one CPS golden rectangle equivalent:

    Figure 6.4: One CPS Golden Rectangle
    Figure 6.4

    Two more CPS golden rectangles can be seen in the icosahedron pattern. These three golden rectangles fully define the vertices of the icosahedron pattern in CPS - see Figure 6.4-1 below:

    Figure 6.4-1: Three Orthogonal CPS Golden Rectangles
    Figure 6.4-1

    The value of the CPS equivalent of the golden number for this icosahedron pattern can be calculated as the ratio between the numbers of small squares that define the CPS golden rectangle (26 divided by 16) and is equal with 1.625

    These two numbers (16 and 26) can be used as the first two terms of a Fibonacci sequence:

    16, 26, 42, 68, 110, ...

    Icosahedron patterns defined by CPS golden rectangles with higher terms from the Fibonacci sequence defined above will generate CPS golden numbers closer to the value provided in section 6.1.

    Explore the links below for three 3-D views of golden rectangles in CPS icosahedron patterns:


  • 6.5 Nested Triangles in CPS (Fibonacci Sequences vs The Golden Section)

    The second definition of the golden section provided in section 6.1 can also be extended to CPS. This definition is based on ratio between the diagonal and the length of a regular pentagon and is close related to the fact that pentagons can be infinitely nested - as shown in Figure 6.1-1

    The eight faces of the icosahedron that have an underlining hexagonal lattice can also define nested triangle - see Figure 6.5 below for a visualization of this fact:

    Figure 6.5: Nested Triangles - hexagonal lattice
    Figure 6.5

    The number of struts needed to construct such nested triangle can be interpreted as being terms of a Fibonacci sequnce. For the example provided above this sequnce is:

    7, 9, 16, 25, ...

    Figure 6.5-1 shows another set of nested triangles defined by the following Fibonacci sequence:

    6, 8, 14, 22, ...

    Figure 6.5-1: Nested Triangles CPS Pattern
    Figure 6.5-1

    Again, as stated before, nested triangles defined by higher terms from the Fibonacci sequences can be constructed in CPS that generates CPS golden numbers closer to the value provided in section 6.1.


7. Pythagoras's Theorem

CPS Facts

At first glance, it looks like we don’t have to proove the Phytahgorean Theorem in CPS. After all, CPS only considers some points from the Euclidian 3-D space, namely those points obeying the close-packing of spheres constarains. Pythagoras's Theorem is true for all the points in the 3-D space, so it has to be true for the points that make-up the CPS arrangement.

Descartes’ analytical geometry does not provide any proof that the distance between two points in the Cartesian plane can be calculated using Pythagoras's Theorem. He simply assumes and postulates this to be true and continue from there.

There are hundreds of proofs (in the Euclidian Geometry) for the Pythagoras's Theorem. The one presented below is a classic and shows the connection between the Pythagoras's Theorem and the Golden Section.

Figure 7.0: Pythagoras's Theorem - A Classical Proof
Figure 7.0

A real life way of looking to the Pythagoras's Theorem could be stated like this: If the distances between the front legs and back legs of three horses form a right triangle, then the surface of the image of the biggest horse is equal with the sum of the images of the surfaces of the smaller horses - see Figure 7.1 below:

Figure 7.1: Pythagoras's Theorem
Figure 7.1

Having said that, one cannot resist the temptation of looking for facts in the CPS, facts that might provide another kind of explanation of the validity of the Pythagorean Theorem - that is what we will start doing in this remaining of this section. Future releases of this document will add more facts to support this - as these facts are ready for publishing.


  • 7.1 Square-Roots Spiral and Rhombic Dodecahedron

    The square root spiral, also known as the spiral of Theodorus in the Euclidian geometry, is a spiral composed of right triangles having the hypotenuses equal with the square root of natural numbers - see Figure 7.1 below:

    Figure 7.1: Square-Roots Spiral
    Figure 7.1-0

    Plato mentioned Theodorus’ spiral in the Theaetetus dialog and also mentioned that Theodorus proved that all the square roots of non-square integers are incommensurable among themselves.

    From Euclidian geometry it is also known that the diagonals and the sides of the rhombic dodecahedron have a similar property - see Figure 7.1-1 below:

    Figure 7.1-1: Rhombic Dodecahedron Face
    Figure 7.1-1

    As seen in Section 4.1 the rhombic dodecahedron pattern has a well-defined presence in CPS. Using the face of the rhombic dodecahedron in Euclidian geometry and CPS we can introduce a metrics in the CPS - see Figure 7.1-2 below:

    Figure 7.1-2: CPS Metrics - Case 1
    Figure 7.1-2

    For higher frequencies rhombic dodecahedrons a scale factor is needed - see Figure 7.1-3 below:

    Figure 7.1-3: CPS Metrics - Case 2
    Figure 7.1-3

    The square root of 5 can also be found in the rhombic dodecahedron as being the line connecting a vertex of the rhombic dodecahedron with the center of the adjacent face. The line goes inside the rhombic dodecahedron - see Figure 7.1-4 and Figure 7.1-5 below:

    Figure 7.1-4: CPS Metrics - Case 3
    Figure 7.1-5

    Figure 7.1-5: CPS Metrics - Case 4
    Figure 7.1-4

    The two rhombic faces depicted in the figures (the first one with the size equal with square root of 3 and the second one which center is represented above), are orthogonal.


  • 7.2 CPS Metric - Surface vs. Length

    Greeks used the surface (the area) as the fundamental concept in geometry, not the line (the length). This aligns very well with Pythagoras Theorem - the theorem proves a relationship between surfaces, not lengths.

    Step 1 (Square Area = 1):

    The square with an area of 1 is the unit element. Explore the link below for a 3-D visualization of the square in CPS with an area equal with 1:

    Figure 7.2 below shows the numerical values of the quantities involved:

    Figure 7.2: Square Area=1 in CPS
    Figure 7.2-0

    Step 2 (First Lines):

    The lengths of the sizes of this square are also 1. Explore the links below for a 3-D visualization in CPS of the length of 1, and its corresponding line:

    Again, Figure 7.2-1 below shows the numerical values of the quantities involved in defining this length:

    Figure 7.2-1: Length=1 in CPS
    Figure 7.2-1

    In the CPS one can identify an infinite number of lines types – spanning in all directions. Each such type of line corresponds to a square root number. Figure 7.2-2 and Figure 7.2-3 show the first two of these lines in the CPS:

    Figure 7.2-2: Line coresponding to square root of 2
    Figure 7.2-2

    Figure 7.2-3: Line coresponding to 1
    Figure 7.2-3

    Step 3 (Square Area = 2):

    Explore the link below for a 3-D visualization of the square in CPS with an area equal with 2:

    Figure 7.2-4 below depicts the quantities involved in defining and determining this square:

    Figure 7.2-4: Square Area=2 in CPS
    Figure 7.2-7

    Step 4 (More Lines):

    The line corresponds to the square root of 3 is represented below - see Figure 7.2-5:

    Figure 7.2-5: Line coressponding to square root of 3
    Figure 7.2-4

    The line corresponds to the square root of 5 is represented below - see Figure 7.2-6 and Figure 7.2-7:

    Figure 7.2-6: Line coressponding to square root of 5 - Case 1
    Figure 7.2-7

    Figure 7.2-7: Line coressponding to square root of 5 - Case 2
    Figure 7.2-6

    There are 24 (square root of 5)-lines emanaiting from a point/sphere in CPS. The directions of these lines are given by the vertices of the truncated octahedron - see Figure 7.2.-8 below:

    Figure 7.2-8: Truncated Octahedron
    Figure 7.2-8

    Step 5:

    This process can be continued. CPS has the property of supporting lines for the square root of any natural number. The square roots of the natural numbers determine the steps, or the units of these CPS lines.

    Each such line can be associated with a surface that defines a CPS plane . These CPS planes can be imagined as having an underlining square lattice with the corresponding size (the square of the corresponding line step).

    The CPS planes are oriented after all directions possible. CPS planes corresponding to non-square integers are not parallel among themselves.


  • 7.3 Pythagoras's Theorem in CPS Space

    This section provides a way of understanding the relationships between squares of increasing surface area in the Euclidian geometry and then applied these facts to the CPS space.

    Step 1:

    Let’s consider the Euclidian plane and two squares, the square ABCD with an area equal with n, and the square MNOP with an area of n+1 – see figure below 7.3 below:

    Figure 7.3: From Square n to Square n+1 - Case 1
    Figure 7.3-0

    The difference between MNOP and ABCD can be decomposed in 4 squares and 4 rectangles – see figure above. The length x can be determine by finding the positive root of the second degree equation:

    Formula 011

    Note that x decreases when n increases - see table and graph below:

    Formula 012

    Step 2:

    Let’s consider again the Euclidian plane and the square ABCD and extend it with x in four orthogonal directions – as shown in the figure below:

    Figure 7.3-1: From Square n to Square n+1 - Case 2: Step 1
    Figure 7.3-1

    The following four equal right triangles have been formed: AMN, BNP, COM and DPO.

    Formula 013

    Let's consider:

    Formula 014

    The sum of all four triangles is:

    Formula 015

    And then we have:

    Formula 016

    Step 3:

    Let’s consider now the square MNOP and extend it with y in four orthogonal directions – as shown in the figure 7.3-2 below:

    Formula 017

    Figure 7.3-2: From Square n to Square n+1 - Case 2: Step 2
    Figure 7.3-1

    The following four equal right triangles have been formed: MXY, NYZ, PZW and OWX.

    Let’s consider:

    Formula 018

    Now, as before, let’s calculate the area of triangle MXY:

    Formula 019

    Let’s consider:

    Formula 020

    The sum of the area of all four triangles (MXY, NYZ, PZW and OWX) is:

    Formula 021

    And then we have:

    Formula 022

    In conclusion the transition from a square with surface n to a square with surface n + 1 takes place in two steps - see Figure 7.3-3 below:

    Figure 7.3-3: From Square n to Square n+1 - Details
    Figure 7.3-1

    Both triangles AMN and MXY have tha same area, equal with 1/2, and independent of n.

    This process can be extended:

    Formula 023

    Step 4:

    As seen in section 6.2, the squares with area of 1, 2, and 3 do not belong to the same plane. This observation and can be extended for any value of n , namely the square with area equal with n and the square with area equal with n+1 does not belong to the same plane and are not parallel with each other.

    The steps presented above can still be applied; one has to consider the transition being done using the unit of length in CPS. The segments AM and MX are in facts projections of the CPS length unit on the lines (directions) that connect the corresponding vertexes of square n and square n+1 .

    The invariant in this process are the unit of length in CPS and the directions of these units - they are always parallel with each other (there is no rotation required in defining the CPS space).

8. Conclusions

Where do we go from here?

We started from two simple assumptions – the points in space are identical sphere of radius dr arranged using close packing rules.

These assumptions were based on the fact, shown elsewhere, that the close-packing of spheres (considered in this document) is the most efficient way of filling-up the space (the principle of the most efficient way of doing something). Also, it can be said that the sphere is the simplest object in the Universe but has the potential of creating an infinite number of CPS patterns.

The approach of looking to space, surfaces and lines presented here could have a major impact on mathematics and science in general. The main impact in mathematics is on calculus, on the notion of continuum, on the complex analysis, and many other branches.

The Cartesian plane and the Cartesian space are also used in science as pseudo-spaces for interpreting the non-spatial measurements and data.

For example one can perform an experiment measuring the changes of temperature over time of a hot metal object sunken in water. After the measurements are done, a graph is plotted in a Cartesian plane using a time versus temperature coordinate system – to show the evolution of this process.

What this does, it takes the time and temperature and applies a variant of similarity theorem by making these two physical quantities equivalent with two orthogonal directions in space (plane).

By this process, the couples (time, temperature) become points in a Cartesian plane. From here, they are treated as normal points in space, and the Cartesian analytical geometry takes over.

Conscious or not, we all have accepted these facts when accepting any theory or interpretation of any type of data. This includes the interpretation of financial data, statistical measurements of any kind, or any other imaginable experimental data ever performed and being later explained or interpreted.

From a pure mathematical point of view the spheres in CPS space are considered infinitesimal (with the radius dr ).

When this geometry is applied to the physical world, the dimension of these sphere are finite – very small and in the range corresponding to Plank’s constant.

For phenomena observed using the human senses, the number of spheres involved is huge, and the spheres can be approximated as being infinitely small.

For phenomena that involve very small quantities, the CPS lattice of the 3-D space becomes critical and the Cartesian space cannot be used anymore.

Quantum mechanics and quantum effects are a consequence of these facts.

The meaning – and the definition of measurement – becomes absolutely essential for quantum mechanics. The incommensurables – discovered by Pythagorean – show that we can imagine geometrical constructions that generate points (and line segments) that are incommensurable with each other – there is no common length unity to measure both of these segments.

We have extended the definition of measurement to quantum mechanics – and expected to get precise results. If the elements of the quantum mechanics experiments - atoms and elementary particle - are equivalent to segments and points of geometrical constructions in CPS – then the quantum mechanics is to be expected. This is the approach we need to take into considerations – to resolve the paradoxes raised by quantum mechanics.

Orientable surfaces are surfaces that preserve right/left handiness. If one left handed creature moves along such a surface it will always be left handed. This has a direct connection with the chemistry - and the existence of the left and right organic molecules. Chemistry of life is able to distinguish between these molecules. We can imply from this that the Universe (the physical space) must be a manifold of orientable surfaces. Mobius type surfaces are not allowed as constituents of the physical universe.

In a way the old Greek idea that the five perfect bodies – the Platonic Solids – are the fundamental blocks of everything – is not so simplistic, or naive. Platonic Structures – the structures obtained from the close packing of spheres – can generate all these five perfect bodies, all 13 Archimedean bodies and a lot more.



This is a live document. Please provide feedback and check back soon for updates!
Ottawa, Ontario, Canada
© 2016-2021 Platonic Structures Inc. All right reserved.

Get in Touch

“If you have an apple and I have an apple and we exchange these apples then you and I will still each have one apple. But if you have an idea and I have an idea and we exchange these ideas, then each of us will have two ideas." George Bernard Shaw

* Required

Choose your Color